点击进入!

在所著Skin in the Game一书中，提出了以下思想实验（我对其略微作了修改）。

100个人去娱乐场，每个人带去玩的钱都一样。有人会输，有人会赢。当这天结束时，我们只需通过计算回来的人口袋里剩下多少钱来算出回报，就可以推断出“优势”是多少。由此我们就能判断出娱乐场的赔率定价是否正确。让我们假设第28位玩家输掉了所有钱。第29位玩家会因此受到影响吗？不会。

你从自己的样本中就可以很确定地算出大约1%的玩家最终会破产。如果你继续不间断地去娱乐场玩，预计也会得到同样的比例——在那段时间内1%的玩家会破产。

现在，假设你只会连续一百天去娱乐场玩，开始时有固定的金额。第28天你输光了所有钱。第29天你还有得玩吗？你没法再玩下去了。不管你的运气有多好，你都可以确定自己最终破产的概率为100%。

前一个例子中那群人的成功概率并不适用于你。我们可以将第一组称作集合概率，第二组称作时间概率（因为第一组的数据是从一群人中收集的，而第二组是一段时间内的单人数据）。读完上述内容后，以后当你阅读博彩分析人士或情报商基于长期预期回报撰写的博客文章时，请千万小心。即使他们的预测是正确的，除非有人拥有无限多的资金，否则没人能够获得市场预期回报。他们是在把集合概率和时间概率混为一谈。如果博彩玩家终究不得不因为资金损失而降低投注金额，那么他的回报将脱离理论预期回报，别无其他可能。

当然大家都知道，那些玩纯粹围绕统计算法设计的游戏（比如轮盘赌和花旗骰）的娱乐场玩家最后都无法逃脱破产的命运。那些能力不足的博彩玩家也是一样，最终都敌不过博彩公司设置的抽水。

然而，博彩不同于娱乐场游戏。如果博彩玩家能比设置赔率的人更好地判定“真实”结果概率，那么理论上他们预期是有可能盈利的。

无论如何，塔勒布的思想实验在这方面很实用：哪怕是占有优势的博彩玩家在读到它时也会考虑一下破产的可能性。你可能拥有高超的预测技能，但是如果一连串运气不好的投注让你损失掉所有资金，你也只能到此为止了。“新的一天”不会到来。

因此，我将在本文的剩余部分中花些时间谈谈优势博彩玩家面对的破产风险。

衡量优势博彩玩家

博彩是的结合。我们如何才能知道博彩玩家的决定中有一定技能含量？去年，我探讨了运用统计数据检验——，它或许能帮助我们回答这个问题。关于博彩玩家是否拥有预测技能，是否有能力获得长期盈利预期——该检验在本质上实际无法直接告诉我们答案。

它只能计算只有偶然性在起作用的情况下，一组利润和损失发生的可能性。不过，如果可能性很小，统计学家会开心地信心大增，认定发挥作用的可能并不是偶然性。这种情况下运用的典型基准数值包括5%和1%。换言之，如果某个博彩记录偶然出现的概率不到1%，那么我们可以说出现该记录的博彩玩家有可能展示出了某些技能。

如此大胆的预测存在数不清的问题，尤其是的问题：我们常常只看见最好的记录，却看不到所有其他中等水平或者输钱的记录。如果一群人中有100位博彩玩家，最好那位的盈利历史是百里挑一那么罕见——这到底是在释放什么样的信息？不幸的是，我们很少能看见所有人的情况。

尽管如此，我仍会在这篇文章中假设百里挑一的优秀记录在一定程度上证明该博彩玩家拥有优势。真相到底如何也许和之后的内容不太相关。因为靠运气盈利的博彩玩家最终将，所以你可以将下文中的数据考虑为可能发生的最佳情况。

破产的概率

博彩玩家在一系列投注期间遭遇破产的概率有多大？这取决于很多变量，包括博彩玩家自身的技能（或者运气）、投注时长、投注的赔率以及投注本金数额等。博彩玩家能力越强（越少遭遇坏运气？），他们输掉全部资金的可能性就越低，这一点不言自明。

我们还应该明白投注赔率越高，结果的变数就越大。当其他条件不变时，变数越大，潜在利润或损失的范围就越大，风险也越大，破产的概率也会随之增加。而且毋庸置疑，投注本金在总资金中占比越大，一段时间内连续遭遇坏运气导致破产的可能性就越大。

正是因为存在更大的变数，比起在更低赔率上投注的博彩玩家，在更高赔率上投注的人通常也会得到更大比例的回报。换句话说，来自更高赔率的相等回报得到了更多的运气庇佑。这就是为什么赛马情报商（他们通常投注在更高的赔率上）发布的回报高于他们的体育博彩同行（这些人通常投注在更低的赔率上）。

当然，由于同样的原因，情报商联盟排名的榜尾也常常可以看到（由于坏运气的影响）损失更大的赛马情报商。下表显示盈利记录为百里挑一的博彩玩家在不同赔率上投下1,000个投注的利润预期——采用我的得出。

盈利的博彩玩家

下表通过10,000次，演示了不同的1%博彩玩家在不同赔率上使用不同投注本金投下最多1,000个投注时，破产风险如何变化。假设博彩玩家开始时的资金为100个单位，投注本金固定不变。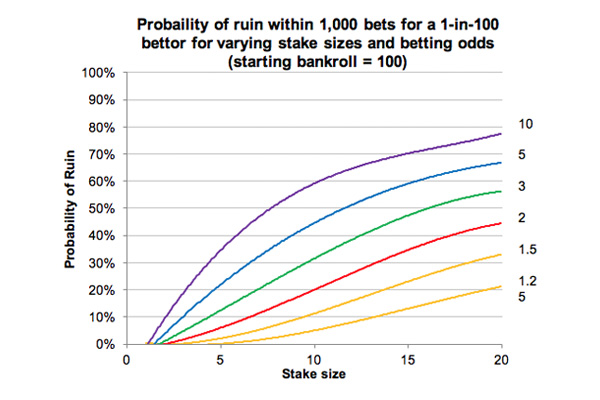

不出所料，更大的投注本金使得破产风险剧烈攀升，特别是投注在更高的赔率上时。假设你喜欢投注在赔率为10的赛马冷门上。尽管理论上你的利润预期超过24%，但是如果你的初始资金为100个单位，而投注本金为10个单位，那么在60%的情况下你永远无法完成1,000个投注。当然，大多数投注冷门的博彩玩家会选择适当地缩减他们的投注本金，但这意味着他们的绝对利润必然会减少。

破产风险管理对绝对利润的影响。

假定我们可以接受的最高破产风险是1%。对于投注在赔率10的博彩玩家来说，如果他们的起始资金为100，那么他们的本金不能大于一个单位。相比之下，投注在低得多的赔率1.25上的博彩玩家可以承受6个单位的本金风险。因此，尽管投注在冷门上的博彩玩家拥有高得多的利润预期，但他们最终的绝对利润和那些投注大热门的博彩玩家的相同。

再举个例子：假设可以接受的破产风险大约为20%。在赔率5上投注的博彩玩家应该投注大约5个单位。相比之下，在赔率1.5上投注的博彩玩家应该投注大约15个单位。前者的利润预期约是后者的三倍。因此，他们的绝对利润预期再一次相同。

这里可以得出一个清晰明确的结论：当博彩玩家的技能水平不相上下时，如果破产风险相同，投注在什么赔率上都不会产生实质影响。因其提供更高的利润预期而只投注更高的赔率，会被减少投注金额来管理增加的破产风险而抵消掉。

破产对预期利润的影响

塔勒布在集合概率vs时间概率的思想实验后引用了沃伦·巴菲特的话：

“先活下来，才有可能成功。”

他以自己的解读评价道：

“破产的存在不允许进行成本效益分析。”

巴菲特和塔勒布是对的。破产改变了预期计算。当我们试图估计预期利润时，我们并不考虑那些因为破产而导致投注过程缩短的情况。上表中的估计利润预期全都计算了1,000个投注。显然，破产概率在非零的情况下，不是所有的都能坚持那么长时间。

假设某位博彩玩家以10个单位的本金投注在赔率2上。他们在1,000个投注中的破产风险为23%。在我的10,000个投注历史模拟中，理论上会破产的情况中有95%都没有停止模拟，继而显示出105.74%的平均投资回报率。但是在现实中，这些利润永远不会发生，因为博彩玩家一旦破产，就只能到此为止了。

如果我们想让真实预期尽可能接近理论预期，就必须尽量将破产风险最小化。最严肃对待博彩的玩家能在直觉上理解这一点，但是我希望文中的分析能够量化这些理念。

非常明显的一点是，哪怕对于技能高超的优势玩家来说，如果想将破产概率控制在远低于1%的水平，投注本金就不能过于超出初始资金的1%。投注赔率越高，占比就应该越小。并且当我们主动思考破产风险时，很显然我们可能选择投注的赔率类型并不会产生实质影响。